우선순위 큐 C언어

프롤로그

우선순위 큐가 어떻게 작동하며 C언어로 구현하는지 개인적으로 공부하여 작성한 공부 노트입니다.

우선순위 큐란?

데이터를 저장할때 우선순위를 가진 데이터를 저장하며 데이터를 꺼낼 때 우선순위가 높은 순으로 데이터를 가져옵니다.

다른 자료 구조와의 차이점

• 스택(Stack) : 가장 최근에 들어온 데이터
• 큐(Queue) : 가장 먼저 들어온 데이터
• 우선순위 큐(Priority Queue) : 가장 우선순위가 높은 데이터

여기서 일반적인 큐(Queue)는 선형적인 형태를 가지고 있지만 우선순위 큐(Priority Queue)는 ‘완전 이진트리’ 형태를 지니고 있으며 최대 힙(heap)을 이용해 구현합니다.

힙(heap) 의 종류

• 최대 힙(Max Heap) : 부모 노드의 키 값이 자식 노드의 키 값보다 ‘크거나 같은’ 완전 이진 트리
• 최소 힙(Min Heap) : 부모 노드의 키 값이 자식 노드의 키 값보다 ‘작거나 같은’ 완전 이진 트리

PUSH, POP 구현

삽입(PUSH) 은 완전 이진트리 형태를 유지하면서 순서대로 데이터를 삽입하는 것 Data1 Data2 Data3.. 왼쪽에서 오른쪽으로

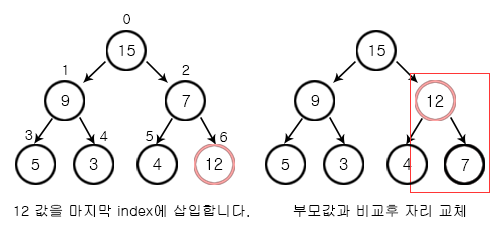
완전 이진트리의 마지막인 (6)index 에 data를 추가합니다.
삽입 이후 루트 노드(0 index 꼭대기) 까지 최대 힙을 구성합니다.

위의 이미지를 예를 들면
마지막 루트(index 6)에 (data 12)를 추가 한 후에
부모 루트(index 2)(data 7) 와 크기를 비교 합니다.
삽입한 노드의 값이 더 크기 때문에 서로 자리를 바꿔줍니다.
이렇게 꼭대기 루트 노드까지 비교하며 올라가며 최대 힙을 구성합니다.

#define MAX_SIZE 10000

// 노드와 노드의 자리를 바꿔주는 함수
void nodeChange(int *a, int *b)
{
  int temp = *a;
  *a = *b;
  *b = temp;
}

// 우선순위 큐 를 구조체 형태로 제작
typedef struct priorityQueue
{
  int heap[MAX_SIZE]; 
  // heap 의 배열형태

  int count;  
  // heap 의 갯수 and 위치값 을 나타내는 값 (index 값이라 보면 된다.)
} priorityQueue;

// 우선순위 큐 삽입 PUSH
void push(priorityQueue *root, int data) 
{
  if(root->count >= MAX_SIZE) return;
  // 만약 priorityQueue 의 노드의 갯수가 설정한 최대값보다 크다면 더이상 값을 추가할 수 없도록 합니다.
  
  root->heap[root->count] = data;
  // data값을 heap의 맨 마지막 트리에 저장
  // 예를 들면 트리가 총 3개가 존재한다면 count값 또한 3 이다.
  // 트리의 index 0 1 2 에 값을 PUSH 한다면 
  // heap[count] = heap[3] 이기 때문에 무조건 마지막에 값이 저장된다.
  // 마지막에 값을 저장하면 index 0 1 2 3 이고 count 값 또한 증가되면서 4 가 된다.
  
  int now = root->count;
  // 추가한 data의 위치값 (index)
  
  int parent = (root->count - 1) / 2;
  // 추가한 data의 부모값
  // 부모값의 위치는 ( 현재 추가한 data 위치값 - 1 ) / 2 를 하면 찾을 수 있습니다.
  
  // 새 원소를 삽입한 이후에 상향식으로 최상단 루트까지 data 값을  힙을 구성합니다.
  while(now > 0 && root->heap[now] > root->heap[parent]) 
  // now > 0 비교하는 값의 위치가 최상단 루트가 될때까지 반복
  // heap[now] > heap[parent] 부모의 data 값보다 현재의 값이 더 크면 실행
  {
    nodeChange(&root->heap[now], &root->heap[parent]);
    // 부모값과 현재 값의 자리를 바꿔준다.
    now = parent;
    // 상향식으로 다시 위 부모 노드와 비교하기 위해서 부모값은 현재가 된다.
    parent = (parent - 1) / 2;	
    // 부모값의 위치또한 다음 검사할 부모값의 위치를 저장한다.
  }
  
  root->count++;
  // PUSH 로 값을 추가하였으니 count 또한 1 증가 시킵니다.
}

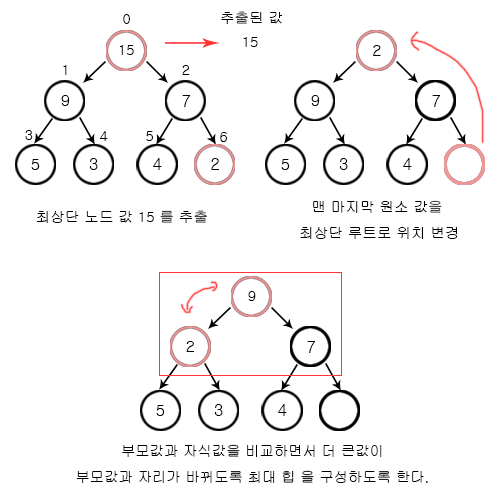
추출 삭제(POP) 가장 위쪽의 루트 노드 값을 제거 한 후에 가장 마지막 원소의 노드의 data 값을 최상단 루트 노드로 위치를 변경 합니다.

최상단 노드(index 0)의 (data 15) 값을 추출 한 후에 맨 마지막 원소(index 6)(data 2) 값을 최산단 노드의 위치로 변경 합니다.
이후 하양식으로 부모 노드와 자식 노드값을 비교하면서 최대 힙 구성을 하도록 내려가며 비교합니다.

결과 확인)

// 우선순위 큐의 추출 POP
int pop(priorityQueue *root) {
  if (root->count <= 0) return -9999;
  // 추출할 대상이 더이상 없을경우 오류를 출력
  
  int res = root->heap[0];
  // 반환할 최상단 루트의 값을 res 변수에 담습니다.
  
  root->count--;
  // 최산단 루트값이 하나 빠짐으로 count 값도 같이 하나 감소시킵니다.
  
  root->heap[0] = root->heap[root->count];
  // 최상단 루트에는 맨 마지막 노드값이 들어가도록 합니다.
  // 이제 최상단 루트와 맨마지막 노드값의 위치가 변경되었으니 하양식으로 data값을
  // 확인해가며 최대힙을 구성해가면 됩니다.
  
  int now = 0, leftChild = 1, rightChild = 2;
  // now 는 최상단 루트의 위치
  // leftChild 최상단 루트의 자식값의 왼쪽
  // rightChild 최상단 루트의 자식값의 오른쪽
  
  int target = now;
  
  // 새 원소를 추출한 이후에 하향식으로 힙을 구성합니다.
  while (leftChild < root->count) {
    if (root->heap[target] < root->heap[leftChild]) target = leftChild;
    // 현재 부모값 보다 왼쪽의 자식값이 더 크면 target 에 자식값을 참조합니다.
	
    if (root->heap[target] < root->heap[rightChild] && rightChild < root->count) target = rightChild;
    // 현재 부모값 보다 외른쪽 자식값이 더 크고 rightChild index 값보다 현재 index 값이 더크면 (index 위치 벗어나지 안도록)
    // target 에 자식값을 참조합니다.

    if (target == now) break; // 더 이상 내려가지 않아도 될 때 종료
        else {
	    swap(&root->heap[now], &root->heap[target]);
	    // 현재 값과 자식값의 자리를 바꿔준다.
	    now = target;
	    // 다음 트리 검사대상을 now에 참조시킵니다.
	    // 그러면 트리를 하양식으로 내려가면서 검사를 계속해서 반복합니다.
	    leftChild = now * 2 + 1;
	    rightChild = now * 2 + 2;
	    // 자식값 index 또한 다음 index 트리로 이동시켜줍니다.
	}
  }
  return res;
}

...CODE...

int main(void) 
{
  int data;
  int n = 5;
  priorityQueue root;
  root.count = 0;

  push(&root, 10);
  push(&root, 20);
  push(&root, 30);
  push(&root, 40);
  push(&root, 50);
  // PUSH 로 차례로 10 20 30 40 50 값을 추가했습니다.

  for(int i = 0; i < n; i++) 
  {
    int data = pop(&root);
    // POP 맨 처음값을 하나씩 추출하여 값을 출력하도록 합니다.
    
    printf("%d ", data);
    // 값을 출력 합니다.
  }
  
  system("pause");
  return 0;
}

결과를 확인해 보면 50 40 30 20 10 순으로 정상적으로 최대 힙이 구성된것을 확인할 수 있었습니다.

에필로그

인강을 보고 여러 블로그도 참조하여 개인적으로 가장 이해할 수 있도록 정리한 노트입니다.
역시 직접 손으로 하나하나 찾아보고 작성해보니 완전히 이해할 수 있었습니다.